Obwohl ich zu Schulzeiten eigentlich ganz gut in Mathe war, habe ich vor allem die Winkelfunktionen nie so richtig verstanden. Ich habe zwar später auch (Wirtschafts-)Mathematik studiert, aber irgendwie habe ich da keine Winkelfunktionen benötigt. Auch bei der Entwicklung des Shops wurde zwar viel Computergeometrie und Winkelfunktionen benötigt, aber die Umsetzung hat mein guter Kollege gemacht, der bereits an der Entwicklung einiger CAD-Systeme beteiligt war und daher blieb mir das erspart.
Neulich habe ich eine Email von meinem Kunden und inzwischen guten Freund bekommen, der für die Erweiterung unseres Shops die Biegeverkürzung berechnen muss.
Das Problem ist eigentlich simpel:
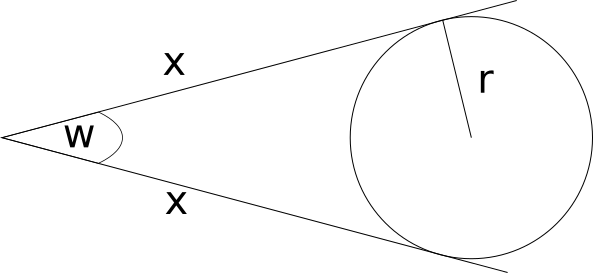
Gegeben sind zwei Linien, die in einem Winkel w zueinander stehen und die beide einen Kreis mit dem Radius r als Tangente berühren. Dabei ist der Abstand zwischen dem Schnittpunkt der Linien und der Tangenten-Punkte gleich lang -> Länge X.
Mit bekanntem Winkel W und Radius r soll die Länge der Strecke X ermittelt werden.
Als mir die Aufgabe gestellt wurde, habe ich erst einmal gar nix verstanden, bzw. wusste auf Anhieb erst mal nicht weiter. Mein großer Sohn hat mir da einen Tipp gegeben. Wenn man eine Linie zwischen dem Linien-Schnittpunkt und dem Mittelpunkt zeichnet, ergeben sich zwei rechtwinklige Dreiecke. Mit der Prämisse, dass die Abstände X auf beiden Seiten gleich sind, ergibt diese Linie die Winkelhalbierende .
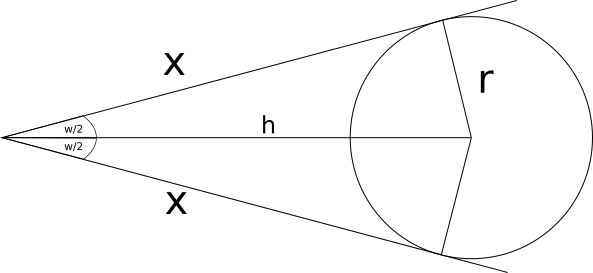
Mit Hilfe des Winkels und einer Seitenlänge kann man mit den Winkelfunktionen die Seitenlänge einer anderen Seite ermitteln.
Es stehen prinzipiell 3 Winkelfunktionen zur Verfügung.
Sinussatz
![]()
in unserem Fall also :
![]()
Cosinussatz
![]()
in unserem Fall also:
![]()
Tangenssatz
![]()
in unserem Fall also:
![]()
Für unseren Fall können wir den Tangenssatz nutzen und nach x umstellen.
So ergibt sich:
![]()
Anhand eines Sonderfalls können wir prüfen, ob der Tangenssatz passt. Wenn die Linien im 90 Grad-Winkel stehen, entspricht die Länge von x genau dem Radius.
Setzt man die entsprechenden Werte in die Formel ein ergibt sich:
![]()
Da der Tangens von 45 Grad = 1 ist, ergibt sich:
![]()
Alternative Berechnung und Herleitung von Tangenssatz
Anhand des Sachverhaltes kann man aber auch den Tangenssatz mit Hilfe des Sinus-Satzes und des Cosinus-Satzes herleiten.
Zur Herleitung wird z.B. das oberste Dreieck genutzt und der Sinus-Satz genutzt.
![]()
wird nach der Hypotenuse umgestellt. Es ergibt sich also:
![]()
Nun nimmt man den Cosinus-Satz:
![]()
und setzt den im Sinus-Satz umgestellten Term für die Hypotenuse ein.
![]()
Nach „Normalisierung“ des Bruchs ergibt sich:
![]()
So ergibt sich:
![]()
bzw.
![]()
Das ist genau der Tangenssatz, d.h. :
![]()
Winkel vs. Bogenmaß
Bei der Berechnung von Sinus, Cosinus und Tangens ist entscheidend, ob der Winkel als „absoluter Winkel“ oder im Bogenmaß angegeben wird. Beim Taschenrechner gibt es drei Modi, der i.d.R. durch die DRG-Taste umgestellt wird. Der „normale Winkel“ Modus ist DEG (D) dort wird der Winkel absolut angegeben, zwischen 0 und 360 Grad. Beim zweiten Modus (RAD) wird ein Winkel als vielfaches von Pi angegeben, dabei ist ein Vollkreis durch
![]()
gekennzeichnet. Die Umrechnung eines Winkels in Bogenmaß ist dabei ziemlich einfach:
![]()
Verschiedene Computerprogramme z.B. auch Excel erwarten Winkel im Bogenmass, so dass ihr die „normalen“ Winkel entweder erst einmal manuell umrechnen müsst, oder durch eine Funktion entsprechend transformieren müsst. In Excel geht das z.B. durch die Funktion: BOGENMASS(Winkel). Bitte achtet bei Excel darauf.
Der dritte Modus GRAD am Taschenrechner ist ziemlich exotisch, dort besteht ein Vollkreis aus 200 Grad. Da das sehr speziell ist, betrachte ich das nicht weiter.
Komisch, dass man, wenn man sich mal wieder mit der Materie beschäftigt und dabei ein praktisches Beispiel hat, das Verständnis doch besser ist, als wenn man das nur in der Schule lernt. Auf alle Fälle habe ich das jetzt verstanden, ich hoffe, mit Hilfe meines Beitrags versteht ihr den Sachverhalt auch besser.


