crypti

crypti

Ich hatte ja vor einiger Zeit angedeutet, dass ich im Zuge des Stahlbauprojektes “S4T” relativ viele Sachen auch in Richtung Computergeometrie zu machen habe, daher auch Dinge, wie Flächeninhalt, etc. ermitteln muss.

Eines dieser Aufgaben war es, den Flächeninhalt und den Umfang eines Rechteckrohres zu ermitteln. Dieses ist an den Ecken jeweils mit einem Radius ro (außen) und ri (innen) abgerundet und besitzt eine Wandstärke t, sowie Höhe h und Breite b.

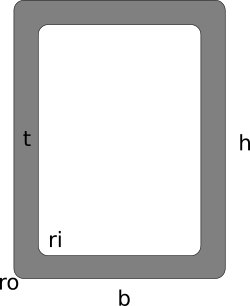
Nach kurzem Überlegen ist die Berechnung des Flächeninhaltes und Umfangs eigentlich gar nicht so schwer. Im Endeffekt ermitteln wir als erstes den Flächeninhalt der Außenfläche und anschließend der Innenfläche und ziehen diese voneinander ab. Übrig bleibt dann der Flächeninhalt der “Wand”.
Fangen wir mit dem Flächeninhalt der Außenkontur an.

Woraus besteht so ein abgerundetes Rechteck? Im Endeffekt aus 4 Viertelkreisen und 3 Rechtecken. Die einzelnen Flächen habe ich mal markiert:

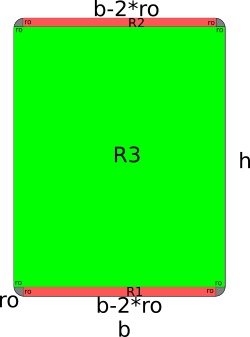
Grau markiert sind jeweils die Viertelkreise, dazu haben wir zwei gleich große Rechtecke (rot)
R1, R2 mit jeweils b-2 \cdot r_{o} Länge und r_{o} Höhe und das grüne Rechteck R3 mit h-2 \cdot r_{o} Höhe und b Breite.

Mit Hilfe dieser Skizze wird es bedeutend einfacher den Flächeninhalt und Umfang auszurechnen.
Berechnen wir erst einmal die Flächeninhalte, die ergeben sich aus der Addition der Flächeninhalte der einzelnen Flächen.
Die vier Viertelkreise ergeben zusammen einen Vollkreis, daher kann die normale Formel zur Berechnung des Flächeninhalts eines Kreises genutzt werden:

A_{kreis} = \pi \cdot r_{o}^{2}

Für die Rechtecke R1 und R2 ergibt sich jeweils:

A_{R1/2} = ( b - 2 \cdot r_{o} ) \cdot r_{o}

da wie oben bereits beschrieben die Rechtecke eine Höhe von r_{o} und eine Länge von b - 2 \cdot r_{o} besitzen.

Last but not least wird der Flächeninhalt des dritten Rechtecks ermittelt:

A_{R3} = b \cdot (h - 2 \cdot r_{o})

So haben wir alle Flächeninhalte, diese werden summiert, dann ergibt sich also folgende Gleichung:

A_{außen} = A_{kreis} + A_{R1} + A_{R2} + A_{R3}

A_{außen} = \pi \cdot r_{o}^{2} + 2 \cdot ( b - 2 \cdot r_{o} ) \cdot r_{o} + b \cdot (h - 2 \cdot r_{o})

Easy. Nun noch der Umfang. Der Umfang der 4 Viertelkreise ergibt wiederum den Umfang eines Vollkreises.

U_{kreis} = 2 \cdot \pi \cdot r

Nun werden noch jeweils die Außenseiten der drei Rechtecke hinzuaddiert, d.h. je einmal die Breite von R1 und R2 (b - 2 \cdot r_{0}) und zwei mal die Höhe von R3 ( h - 2 \cdot r_{0})

Also ergibt sich :

U_{außen} = 2 \cdot \pi \cdot r_{o} + 2 \cdot (b - 2 \cdot r_{o}) + 2 \cdot (h - 2 \cdot r_{o})

Das könnte man jetzt noch ausmultiplizieren, aber dazu bin ich gerade einfach zu faul.
Im Endeffekt haben wir so erst einmal Flächeninhalt und Umfang der Außenkontur.
Auf gleiche Art und Weise kann man das auch mit dem inneren abgerundeten Rechteck machen. Hier ist zu beachten, dass Breite und Höhe jeweils um 2 \cdot t kleiner sind.
Daraus ergibt sich dann:

A_{innen} = \pi \cdot r_{i}^{2} + 2 \cdot ( b - 2 \cdot t - 2 \cdot r_{i} ) \cdot r_{i} + (b - 2 \cdot t) \cdot (h - 2\cdot t - 2 \cdot r_{i})
U_{innen} = 2 \cdot \pi \cdot r_{i} + 2 \cdot (b - 2 \cdot t - 2 \cdot r_{i}) + 2 \cdot (h - 2 \cdot t - 2 \cdot r_{i})

Für den Flächeninhalt der Wandfläche kann nun die Innenfläche von der Außenfläche abgezogen werden.
Wenn man dann noch die Länge des Rohres hat, kann man so ganz einfach das “Materialvolumen” mit der entsprechenden Dichte des Materials (z.B. 7,85 \frac {g}{cm^{2}}) sogar das genaue Gewicht des Rohres ermittelt werden.

Schreibe einen Kommentar

Artikel, die Dir auch gefallen könnten

Remote-Desktop unter Manjaro

Hallo da draußen, Leute die mich etwas besser kennen, wissen, dass ich ein großer Fan von Manjaro Linux bin. Ich nutze das schon seit etlichen

mehr...
September 13, 2023 Keine Kommentare

Linux und Active Directory

Hallo Welt da draußen, heute bin ich mal wieder fast verzweifelt. Ein bisschen habe ich mich an meine Zeiten als Angestellter mit dem Projekt der

mehr...
Oktober 21, 2022 Keine Kommentare